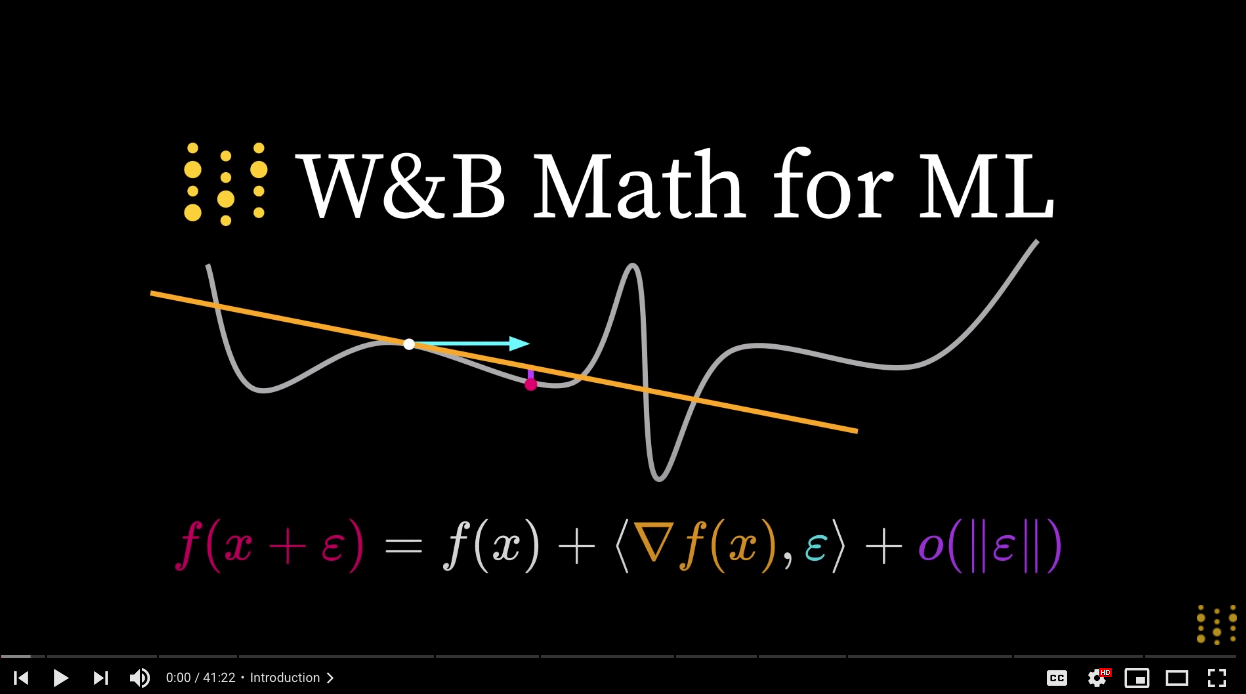Posts
-
Reckoner Bundles: A Riddler's Inway
This gloss of a key passage from “Computer Systems: A Programmer’s Approach” is inspired by Poul Anderson’s “Uncleftish Beholding”.
A reckoner bundle is made of hardware and bundlish software that work together to run wending riddlelists.
Enlightenment within the reckoner is forstood as clusters of twines (short for two rimes) that are understood in unlike ways, depending on the background.
-
At the Intersection of LLMs and Kernels - Research Roundup
Relational databases like postgreSQL and operating system kernels like Linux are foundational building blocks for computing systems. Every “application” is in essence an “application” of those building blocks to some purpose: Twitter applies databases to write and read tweets; it applies an operating system to operate the hardware required to do so.
Large language models – and large generative models of complex data types more broadly – are a new building block at this foundational layer. ML researchers like me have many useful intuitions about what can be built with this novel building block and how to improve it.
But the people who have spent years building with those other blocks have many more. Many of these inuitions are surprising to someone who has spent more time with neural networks than with the network stack.
This post is a collection of short explainers for papers that directly draw from systems metaphors in designing improvements for LLMs, ranging from novel approaches to pretraining to inference-time speed optimizations.
Perhaps most interesting are prompting strategies that make LLMs act more like kernels.
It is intended to get researchers and hackers of LLMs interested in systems and vice versa.
-
Reckoner Riddlelisting in Rust
Here’s a Rust Riddlelist that bids the world hello:
fn main() { println!("Hello, World!"); }Let us walk through the words of this riddlelist step by step and come to ken how it drives the reckoner to weave a greeting.
-
Running an LLM on one machine: GLM-130B
tl;dr
- GLM-130B is a GPT-3-scale and quality language model that can run on a single 8xA100 node without too much pain. Kudos to Tang Jie and the Tsinghua KEG team for open-sourcing a big, powerful model and the tricks it takes to make it run on reasonable hardware.
- Results are roughly what you might expect after reading the paper: similar to the original GPT-3 175B, worse than the InstructGPTs.
- I’ve really been spoiled by OpenAI’s latest models: easier to prompt, higher quality generations.
And
- It’s hard to self-serve LLM inferences cheaper than OpenAI will sell them to you.
-
Lecture on Ethics in Tech, ML, and AI
-
Lecture on Troubleshooting & Testing
-
🥞 Full Stack Deep Learning 2022 Labs
-
Reading Group on "Designing ML Systems"
In this book, you’ll learn a holistic approach to designing ML systems that are reliable, scalable, maintainable, and adaptive to changing environments and business requirements.
-
Advent of Code in Three Languages
Different programming languages push us to write code differently.
Python pushed me to write clean code.
Rust pushed me to write performant code.
Haskell pushed me to solve problems differently.
-
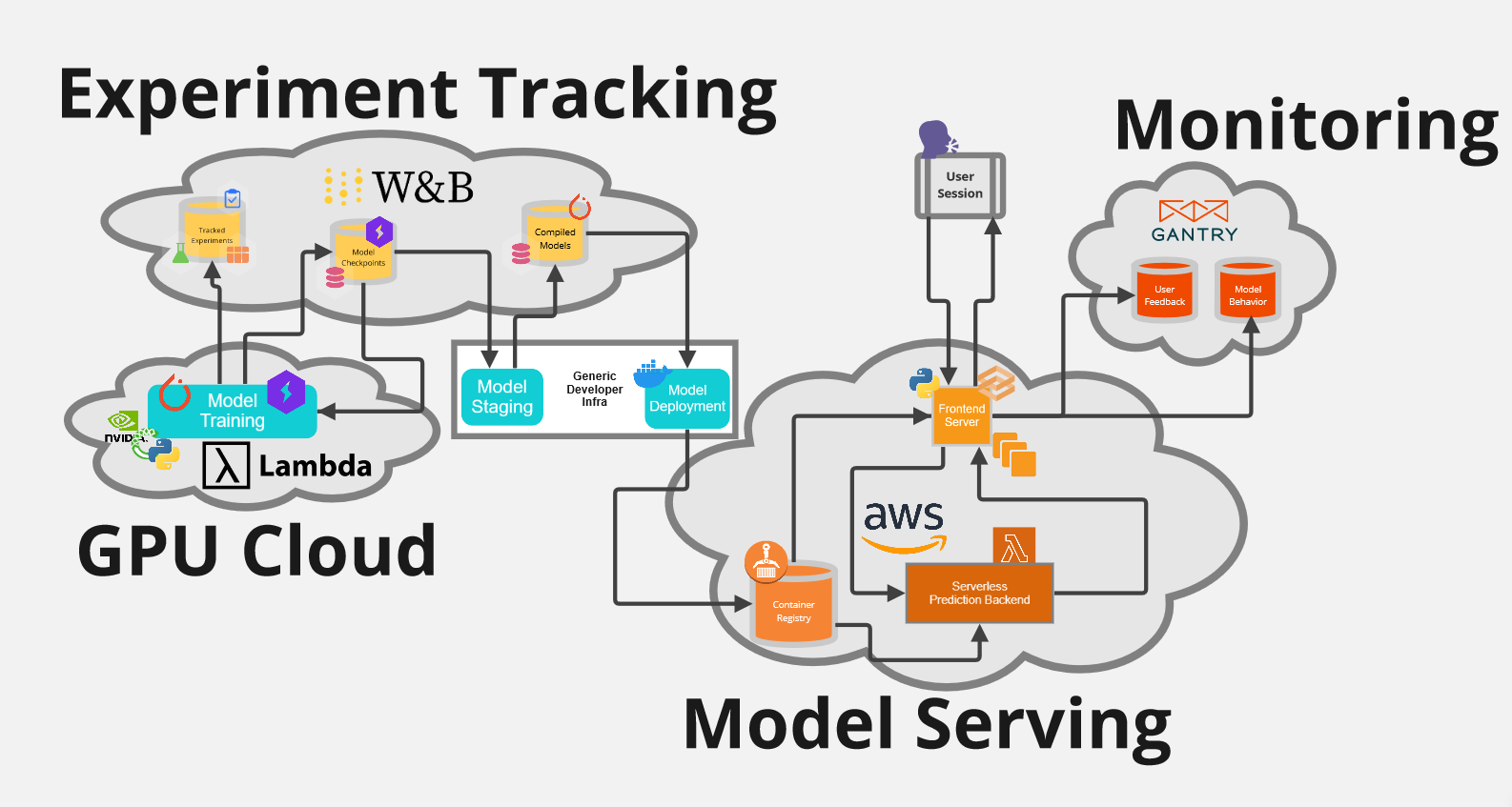
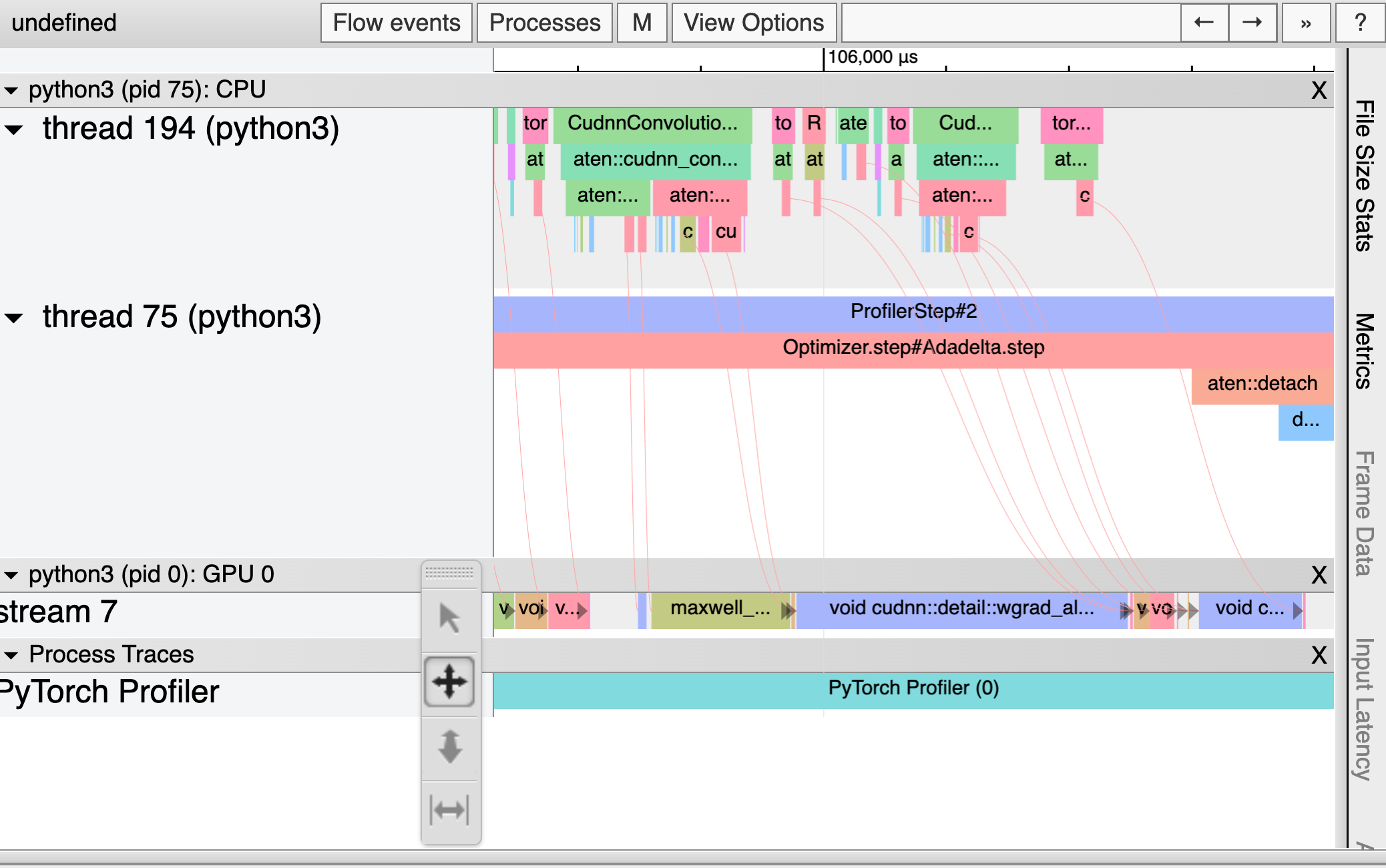
A Public Dissection of a PyTorch Training Step
But now that Weights & Biases can render PyTorch traces using the Chrome Trace Viewer, I’ve decided to peel away the abstraction and find out just what’s been happening every time I call .forward and .backward. These traces indicate what work was being done and when in every process, thread, and stream on the CPU and GPU. By the time we’re done here, we’ll have a clear sense for why most of the optimization tips above work, plus the tools to make more informed choices about the performance of our PyTorch code.
-
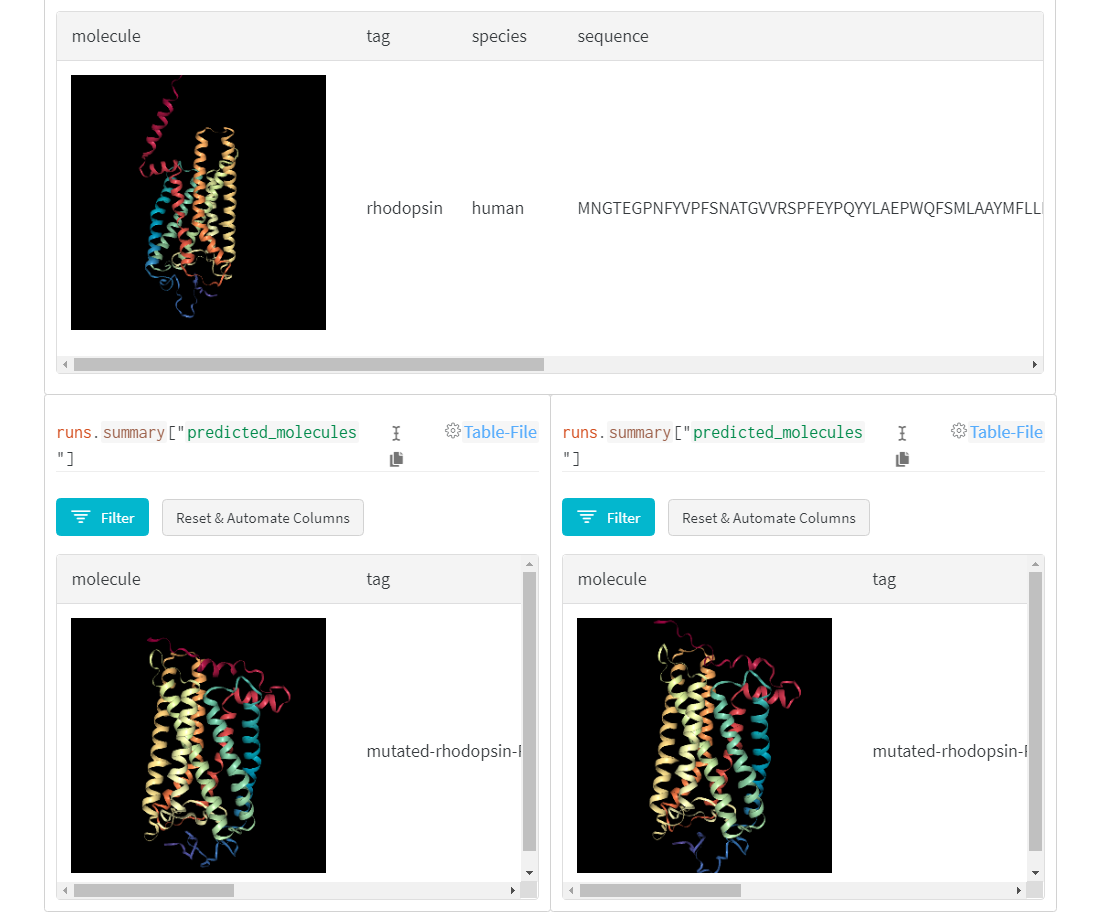
AlphaFold-ed Proteins in W&B Tables
As with tensors, so with proteins: it’s all about the shapes. The genetic code specifies a sequence of chemicals, called amino acids, that are the building blocks of proteins, in turn the building blocks of biological systems. These linear sequences are transformed, millions of times per day per cell in your body, into complex 3D shapes, from molecular motors to molecular scissors, in a process known as protein folding.
-
Online Course on Math for Machine Learning
Contemporary machine learning sits at the intersection of three major branches of mathematics: linear algebra, calculus, and probability.
Today I released the third and final video in my Math for Machine Learning series, which covers core intuitions needed for ML from each of these three toolkits, with an emphasis on the programmers’ perspective. It also includes interactively-graded exercises.
Check the videos out here. Comment on them and let me know what you think!
-
Learn to Use Weights & Biases
Weights & Biases provides developer tools for machine learning – exactly the kinds of tools I wish I’d had while doing my PhD research.
These tools make it easier to track, reproduce, and share ML work, from school projects to research papers to industrial technologies.
I just finished releasing a video series on how to use W&B with some major deep learning libraries. I tried to make them as fun and engaging as possible while still packing them densely with technical info and best practices.
Check the videos out here. Comment on them and let me know what you think!
-
Selectivity and Robustness of Sparse Coding Networks
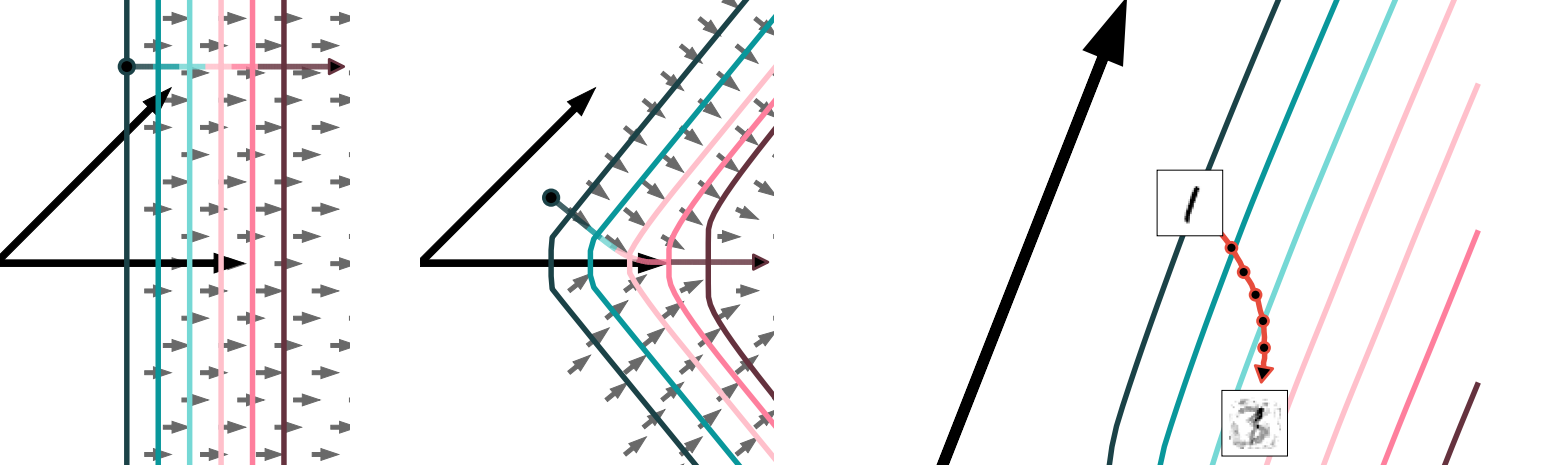
Adversarial attacks on neural networks allow “hacking” of contemporary AI systems: they can be easily convinced that a stop sign is actually a toaster with the right (tiny!) changes to the input.
Humans aren’t so easily fooled, and, as it turns out, neither are some more biologically-plausible but less popular approaches to neural networks, like locally-competitive sparse coding networks.
I worked with Dylan Paiton, Sheng Lundquist, Joel Bowen, Ryan Zarcone, and Bruno Olshausen on understanding why. There seem to be two basic, interrelated ingredients: population non-linearities give more complex response functions and generative models are harder to hack.
Check out the paper here for details.
-
Ph.Done
Today, I delivered my exit talk to the Helen Wills Neuroscience Institute, which means I have officially completed the requirements for the degree of doctory of philosophy in neuroscience!
My dissertation work was on the geometric properties of neural network optimization problems (arXiv paper).
Watch the video here or read the dissertation here.
-
Webinars on Linear Algebra and Vector Calculus
I’ve started doing some short webinars on core math topics in machine learning for Weights & Biases, a startup that offers a really cool experiment tracking, visualization, and sharing tool.
The first webinar, How Linear Algebra is Not Like Algebra, presents Linear Algebra from a programmer’s perspective: every vector/matrix/tensor is a function, shapes are types, and matrix multiplication is composition of functions.
The second webinar Look Mom, No Indices!, introduces an index-free style of computing gradients for functions that take vectors and matrices as inputs. It’s a teaser for this blog post series.
-
A Simple DNN for Identifying Mouse Sleep Stages
-
Gaussians as a Log-Linear Family
\[\begin{align} \nabla_\theta A(\theta, \Theta) &= -\frac{1}{2}\Theta^{-1}\theta = \mu\\ \nabla_\Theta A(\theta, \Theta) &= -\frac{1}{4}\theta\theta^\top\Theta^{-2} - \frac{1}{2}\Theta^{-1} = \mu\mu^\top + \Sigma\\ \end{align}\] -
Short Paper on Square Roots and Critical Points
In the next section, we define an analogous algorithm for finding critical points. That is, we again try to solve a root-finding problem with Newton-Raphson, but this introduces a division, which we reformulate as an optimization problem.
Today a short paper I wrote posted to the arXiV. It’s on a cute connection between the algorithm I use to find the critical points of neural network losses and the algorithm used to compute square roots to high accuracy.
Check out this Twitter thread for a layman-friendly explanation.
-
Tails You Win, One Tail You Lose
I presented the math for this at the #cosyne19 diversity lunch today.
— Megan Carey (@meganinlisbon) March 2, 2019
Success rates for first authors with known gender:
Female: 83/264 accepted = 31.4%
Male: 255/677 accepted = 37.7%
37.7/31.4 = a 20% higher success rate for men https://t.co/u2sF5WHHmyControversy over hypothesis testing methodology encountered in the wild a second time! At this year’s Computational and Systems Neuroscience conference, CoSyNE 2019, there was disagreement over whether the acceptance rates indicated bias against women authors. As it turns out, part of the disupute turned over which statistical test to run!
-
Multiplication Made Convoluted, Part II: Python
import numpy as np class DecimalSequence(): def __init__(self, iterable): arr = np.atleast_1d(np.squeeze(np.asarray(iterable, dtype=np.int))) self.arr = arr def multiply(self, other): return DecimalSequence(np.convolve(self.arr, other.arr)) -
Multiplication Made Convoluted, Part I: Math
Well, actually, this is more right than you think:
— Yann LeCun (@ylecun) October 20, 2018
A multiplication *is* a convolution of one multi-digit number by another one over the digit dimension.
Think about it. -
Fréchet Derivatives 4: The Determinant
\[\begin{align} \nabla \det M &= \det M \cdot \left(M^{-1}\right)^\top \end{align}\] -
Fréchet Derivatives 3: Deep Linear Networks
\[\begin{align} \nabla_{W_k} l(W_1, \dots, W_L) = W_{k+1:}^\top \nabla L(W) W_{:k}^\top \end{align}\] -
Google Colab on Neural Networks
The core ideas that make up neural networks are deceptively simple. The emphasis here is on deceptive.
For a recent talk to a group of undergraduates interested in machine learning, I wrote a short tutorial on what I think are the core concepts needed to understand neural networks in such a way that they can be understood by someone with no more than high school mathematics and a passing familiarity with programming.
Thanks to the power of the cloud, you can check out the tutorial and run the examples. Just check out this link. This time, I chose to use Google’s “Colaboratory”, which is like Google Drive for Jupyter notebooks.
-
Functors and Film Strips
-
Use You Jupyter Notebook For Great Good
As part of this year’s Data Science Workshop at Berkeley, I put on a tutorial on using Jupyter Notebooks: a quick sprint over the basics and then examples for inline animations and videos, embedded iframes, and interactive plotting!
Click the badge above to launch the tutorial on binder. You’ll want to check out the
JupyterNotebookForGreatGoodfolder.Check out the repo it works off of here, where you can find local installation instructions.
-
Hypothesis Testing
$$2+2=5$$ $$2+2\neq5$$ Tails $$0$$ $$0.5$$ Heads $$0$$ $$0.5$$ To celebrate the latest stable version of Applied Statistics for Neuroscience, here’s a tutorial on hypothesis testing, based on the lecture notes for the course. Make sure to check out the whole course if you liked this snippet!
-
Fréchet Derivatives 2: Linear Least Squares
\(\begin{align} \nabla_{W} L(W; x,y) = 2 (Wxx^\top - y x^\top) \end{align}\)
-
Fréchet Derivatives 1: Introduction
\(\begin{align} f(x+\epsilon) = f(x) + \langle \nabla_x f(x), \epsilon \rangle+ o(\|\epsilon\|) \end{align}\)
-
How Long is a Matrix?
\(\begin{align} \lvert\lvert X\rvert\rvert^2_2 = \mathrm{tr}\left(X^\intercal X\right) \end{align}\)
-
Hypothesis Testing in the Wild
Apart from being an interesting exercise in the real-life uses of probability, this example, with its massive gap between the true negative rate and the negative predictive value, highlights the importance of thinking critically (and Bayesian-ly) about statistical evidence.
-
A Differential Equations View of the Gaussian Family
\[\begin{align} \frac{d}{dx}p(x) = -xp(x) \end{align}\] -
The Surprise Game
\(\begin{align} \mathbb{E}\left[ S(x) \right] &= H(p) + D_{KL}\left(p \lvert\rvert q \right) + \log \frac{1}{\sum_{x \in \mathcal{X}} 2^{-S(x)}} \end{align}\)
-
Mixture Models and Neurotransmitter Release
import numpy as np def generate_number_releases(size=1): return np.random.poisson(lam=2.25, size=size) def generate_measured_potentials(size=1): release_counts = generate_number_releases(size=size) measured_potentials = [generate_measured_potential(release_count) for release_count in release_counts] return np.asarray(measured_potentials) def generate_measured_potential(release_count): measured_potential = np.sum(0.4 + 0.065*np.random.standard_normal(size=release_count)) return measured_potential -
Tutorial on Linear Generative Models
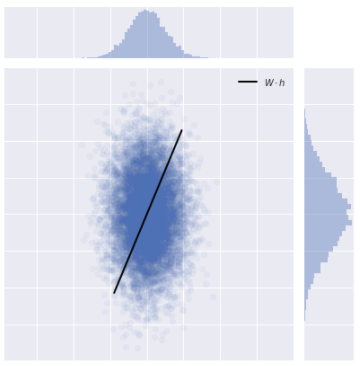
Inspired by the discussion on linear factor models in Chapter 13 of Deep Learning by Courville, Goodfellow, and Bengio, I wrote a tutorial notebook on linear generative models, including probabilistic PCA, Factor Analysis, and Sparse Coding, with an emphasis on visualizing the data that is generated by each model.
You can download the notebook yourself from GitHub or you can click the badge below to interact with it in your browser without needing a compatible Python computational environment on your machine.
-
Graphical Model View of Discrete Channels
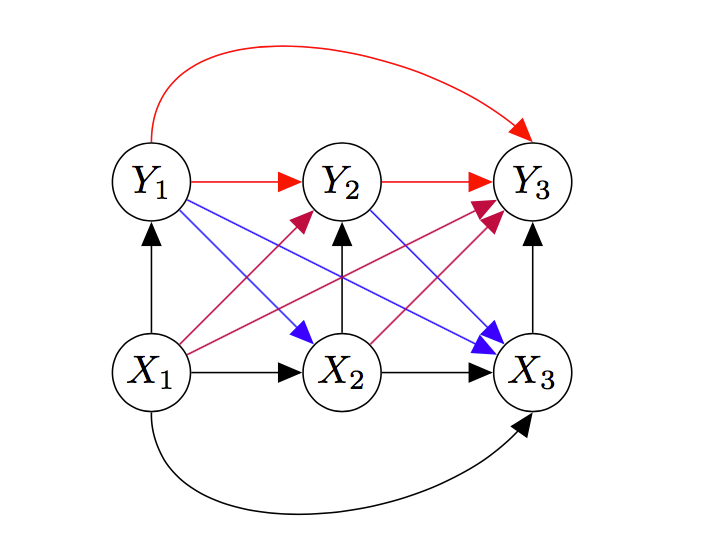
-
Linear Algebra for Neuroscientists
-
Tutorial Notebooks on Machine Learning in Python

Head to this GitHub link to check out a collection of educational Jupyter notebooks that I co-wrote as part of a workshop on data science.
-
Convolution Tutorials Redux \[g * f(t) = \sum_{\tau+\Delta = t} g(\tau) \cdot f(\Delta)\]
Previously, I posted a link to some Jupyter-based tutorials on convolution that I wrote. In order to use them, you needed to install an appropriate computing environment.
Now, thanks to the folks at binder and the magic of the cloud, you can just click this link and use them with nothing more than a web browser.
Neat!
-
Statistics in One Sentence
Statistics is the study of pushforward probability measures from a probability space of datasets to a measurable space of statistics under maps that we call statistical procedures.
-
Paper in Print at Journal of Neurophysiology
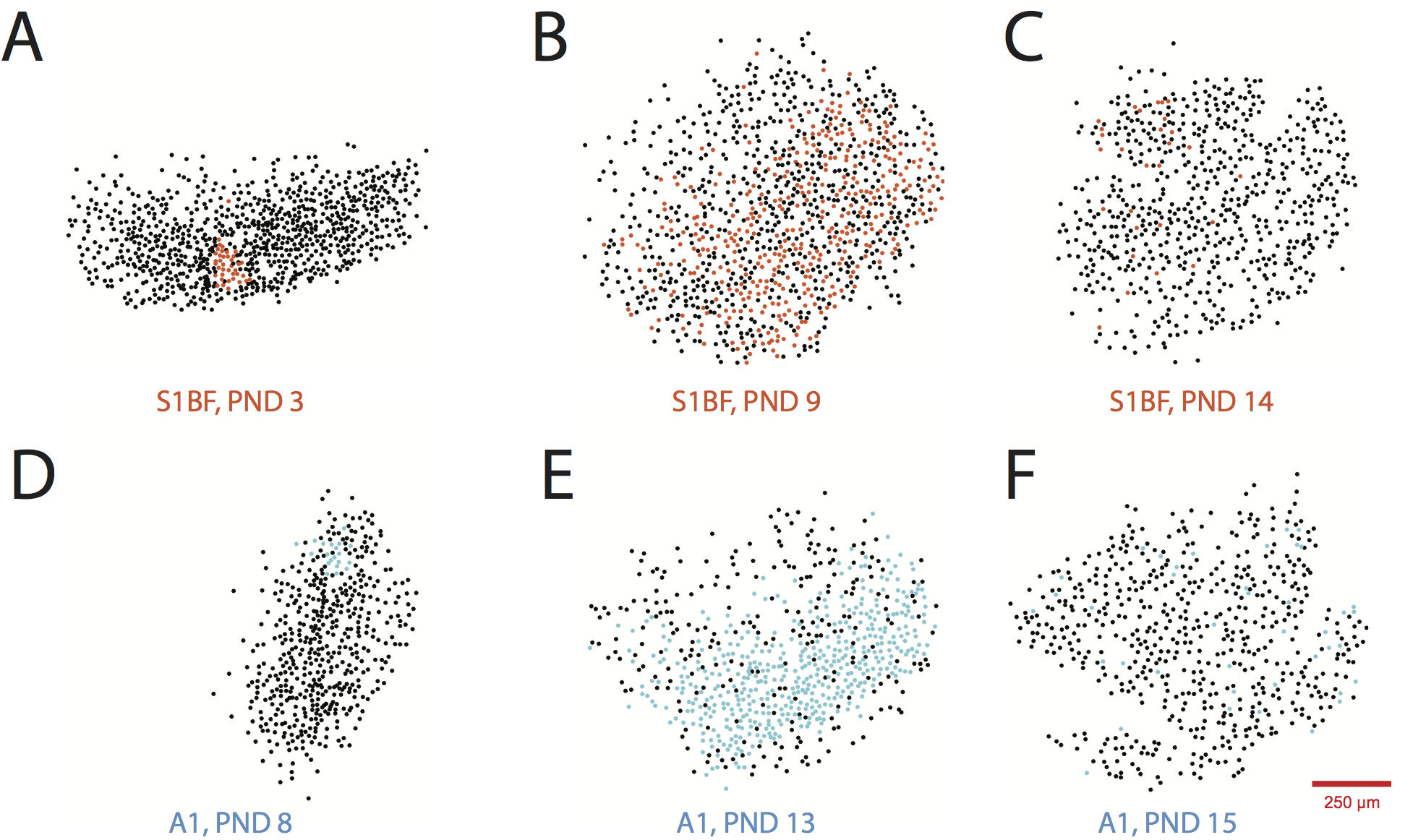
To evaluate the developmental ontogeny of spontaneous circuit activity, we compared two different areas of sensory cortex that are also differentiated by sensory inputs that follow different developmental timelines. We imaged neuronal populations in acute coronal slices of mouse neocortex taken from postnatal days 3 through 15. We observed a consistent developmental trajectory of spontaneous activity, suggesting a consistent pattern for cortical microcircuit development: anatomical modules are wired together by coherent activations into functional circuits.
The final version of my research paper with Jason MacLean on the developmental time course of spontaneous activity in mouse cortex is now available through the Journal of Neurophysiology.
Check it out! You can also read a layman’s summary here.
-
Guest post at Because-Science
…nature adopts a strategy straight out of Saw II: motor neurons are, from the moment they are born, searching frantically for the antidote to a poison that will kill them when a timer runs out. They are, like Biggie Smalls, born ready to die.
Head to Because-Science to check out a fun little guest blog post I wrote explaining the process by which neurons and muscles find each other!
-
What is information theory? What does entropy measure? Mutual information?
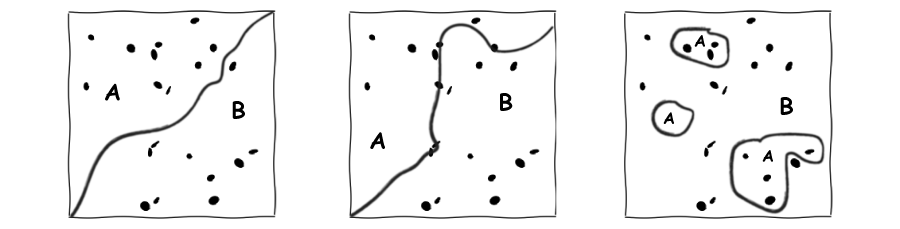
-
Convolution Tutorial IPython Notebooks
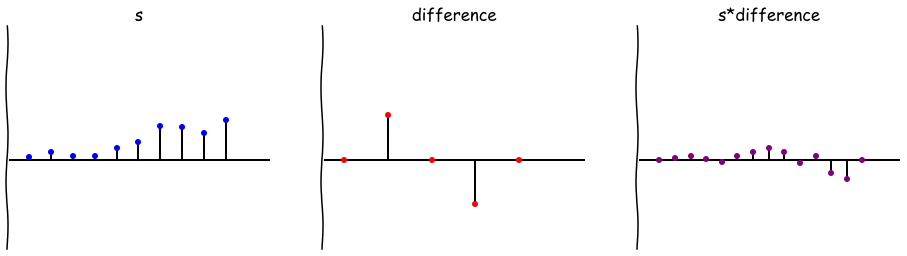
I recently gave a tutorial on convolutions. You can check out the IPython Notebooks at the GitHub repo for Berkeley’s Neuro Data Mining Group.
For more information about the group, check out our website. Come join us if you’re interested!
-
What is Bayes' Rule?
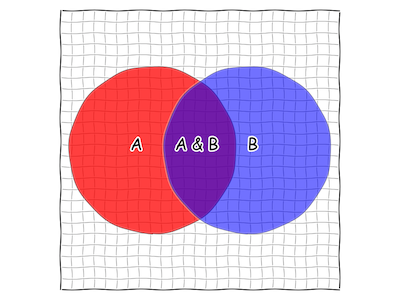
subscribe via RSS