Multiplication Made Convoluted, Part II: Python
import numpy as np
class DecimalSequence():
def __init__(self, iterable):
arr = np.atleast_1d(np.squeeze(np.asarray(iterable, dtype=np.int)))
self.arr = arr
def multiply(self, other):
return DecimalSequence(np.convolve(self.arr, other.arr))
Introduction
Well, actually, this is more right than you think:
— Yann LeCun (@ylecun) October 20, 2018
A multiplication *is* a convolution of one multi-digit number by another one over the digit dimension.
Think about it.
Convolutions show up in many places: in signal processing, in probability, and of course in the marriage of the two, machine learning. Check out this convolution tutorial for more details. They are just as intimately related to such deep and powerful mathematics as the Central Limit Theorem and the Fourier transform as they are to understanding what happens when you shuffle cards.
The above tweets, by satirical convolution fanatic @boredyannlecun and actual convolution fanatic actual Yann Le Cun, reveal an unexpected connection between convolutions and the humble mutliplication operation. I decided to work it out thoroughly and write it up.
In a previous blog post, we worked through the Think about it. phase by first thinking about how we normally do multiplication, then generalizing it, and then deriving the convolutional form.
In this blog post, we’ll work through implementing a number type in Python that actually makes use of this relationship to do multiplication. Along the way, we’ll learn how to hook into Python’s built-in operators with our own objects using what are called, almost without hyperbole, magic methods.
Multiplication, Convolution, and Sequences of Digits
To think of a multi-digit number, like \(x=12345\), as something with a “digit dimension” is to think of it as a one-dimensional vector:
If we want to convert that vector back into the original number, we add up the entries, with each multiplied by \(10\) to some power:
The previous blog post showed how, in this representation, we can write multiplication as
which is the form of a convolution!
First Pass Implementation
In order to implement our multiplication algorithm in Python, we’ll need to make some inter-related choices: how do we represent our sequences of digits, how much of the possible functionality of numbers do we want to implement, and what do we roll ourselves versus crib from libraries.
The lowest-effort choice is to say that we will treat any sequence as a digit sequence,
only implement a multiplication algorithm,
and use the built-in numpy function convolve.
The result is admirably terse:
import numpy as np
def multiply_digit_sequences(a, b):
return np.convolve(a, b)
multiply_digit_sequences([1, 2], [3])
array([3, 6])
The benefit of this approach is that the user can hook into all of the rich functionality of the types accepted by the convolve function,
like iteration and built-in functions.
But if we’re implementing our multiplication algorithm as part of a broader project that uses sequences of decimal digits, then this leaves a lot to be desired.
First, there’s nothing to stop a user providing any input that’s valid for np.convolve as input to this function.
For example, a vector of floating point numbers, which is difficult to interpret as a sequence of digits.
Second, we don’t have a good way to test this small nugget of code, always necessary in a larger, multi-user project, and doing so will add a bunch of heft that takes away the advantage this approach as in brevity.
Third, our function isn’t particularly user-friendly or extensible:
we rely on the user to decide how an array matches onto a decimal sequence.
For example,
one person using the above might presume sequences are stored
in the order they are read and written,
as in
while another, thinking in terms of list indices, might presume sequences are in order of increasing power of the base, as in
\[12345 \rightarrow \left[5, 4, 3, 2, 1\right]\]The function will work for each user separately, but if they build any additional functions and try to share them, they are liable to run into unexpected errors.
class Consciousness
We can solve all of these problems by building a class for our sequences:
a collection of related functions and data.
Inside this class,
we can validate inputs separately from our multiplication operation,
add functionality to make testing easy for ourselves and others,
and express our assumptions about what it means to be a sequence of digits.
We begin with the simplest version of this class.
Every class needs a method called __init__, short for initialize.
This method gets called when a member of the class is created.
The presence of two underscores __ (pronounced dunder by some) at the beginning and the
end of this method’s name indicates that it is a magic method.
While other Python functions and methods need to be explicitly called, as in f(argument, other_argument), magic methods get invoked by special syntax.
In the case of the __init__ for ClassName,
that special syntax is ClassName(argument, other_argument)
(don’t forget that Python methods have an “invisible” first argument,
typically called self,
that refers to the object whose method is being called).
The code block below implements an __init__ method
and multiplication for a DecimalSequence type.
In our __init__ method, we allow the user to provide any iterable,
or object over which we can iterate (e.g., a list),
but then convert it to a numpy array of integers.
import numpy as np
class DecimalSequence():
def __init__(self, iterable):
arr = np.atleast_1d(np.squeeze(np.asarray(iterable, dtype=np.int)))
self.arr = arr
def multiply(self, other):
if not isinstance(other, DecimalSequence):
raise TypeError("can't multiply DecimalSequence by object of type:"
.format(type(other)))
return DecimalSequence(np.convolve(self.arr, other.arr))
We implement our multiplication algorithm with a method called multiply,
which takes an input, verifies it is another DecimalSequence,
and then applies convolve to (the arrays of) both sequences.
We haven’t yet added any of the nice features described above.
Before we do that, let’s try out our DecimalSequence type.
The multiplication works well,
if you know that the data is stored in the .arr attribute:
DecimalSequence([1, 2]).multiply(DecimalSequence([3])).arr
array([3, 6])
but if you don’t, trying to look at your answer gives something unusable:
print(DecimalSequence([1, 2]).multiply(DecimalSequence([3])))
DecimalSequence([1, 2]).multiply(DecimalSequence([3]))
<__main__.DecimalSequence object at 0x7f81c0671780>
<__main__.DecimalSequence at 0x7f81c0671748>
Because we made this class ourselves, Python has no idea how to display it.
Furthermore, it’s usually expected that a number type works with the relevant operators,
like +, *, etc.
If someone tries that with one of our DecimalSequences, they get an error:
DecimalSequence([1, 2]) * DecimalSequence([3])
TypeError: unsupported operand type(s) for *: 'DecimalSequence' and 'DecimalSequence'
And there are lots of built-in operations one might want to use that we’ve lost access to by switching from numpy arrays to DecimalSequences:
4 in DecimalSequence([1, 2])
TypeError: argument of type 'DecimalSequence' is not iterable
Do You Believe in Magic?
The solution to all of these problems is magic!
Lots of Python syntax, like mathemetical operators and iteration, can be extended by means of magic. All you need is to know the magic word (not “please”, unfortunately).
For multiplication, the magic word is __mul__.
For printing and sending to the standard out (Out[ii]:), the magic words are
__str__ and __repr__, respectively.
For a fully-fledged iterable, we need three magic words:
__iter__ which gets called by things like in that try to loop, or iterate, over our object,
__len__, which gets called by the len built-in function, and
__getitem__, which we can use to index and slice into our object.
The code block below implements these magics by “stealing” them from the array in .arr.
class DecimalSequence():
def __init__(self, iterable):
arr = np.atleast_1d(np.squeeze(np.asarray(iterable, dtype=np.int)))
self.arr = arr
self.base = 10
def __iter__(self):
"""magic called when we iterate over `self`, e.g. in a `for` loop"""
return self.arr.__iter__()
def __len__(self):
"""magic called by the `len(self)`"""
return self.arr.__len__()
def __getitem__(self, index):
"""magic called by the expression `self[index]` and slicing"""
return self.arr.__getitem__(index)
def __repr__(self):
"""magic called when self is sent to stdout"""
return self.arr.__repr__()
def __str__(self):
"""magic called by `print(self)`"""
return " + ".join(reversed(
["{}*{}**{}".format(val, self.base, k)
for k, val in enumerate(reversed(self))]))
def __mul__(self, other):
"""magic called by the expression `self * other`"""
if not isinstance(other, DecimalSequence):
raise TypeError("can't multiply DecimalSequence by object of type:"
.format(type(other)))
return DecimalSequence(np.convolve(self, other))
A few things to notice:
- The magics
__str__and__repr__seem redundant, since both are string representations of our object.__str__is typically for communicating to users, while__repr__is for debugging and communicating to programs. - The
__str__method makes use of the built-inreversedapplied to our object. Implementing the iterable magics gave us access to this built-in for free! Magic begets magic. - Our
__mul__method also makes use of iteration: it just passesselfandother, rather thanself.arrandother.arr, toconvolve. This works becauseconvolveknows what to do with an iterable, where it wouldn’t have known what to do with our first draftDecimalSequence.
Now, the simple operations defined above work!
print(DecimalSequence([1, 2]) * DecimalSequence([3]))
4 in DecimalSequence([1, 2])
3*10**1 + 6*10**0
False
Trust, but Verify
Our DecimalSequences are now much more usable,
but they are still missing documentation and verification.
For example, if a user provides an invalid input, like [-1, 1],
the multiplication proceeds without complaint:
DecimalSequence([-1, 1]) * DecimalSequence([1, 1])
array([-1, 0, 1])
While this is in some sense the right answer,
our result is no longer a DecimalSequence in that it cannot be written
in the string format we usually write our numbers in.
We can rectify this by adding some validation to the beginning of our class.
In the code block below,
we define a method check_iterable that verifies that the iterable matches our assumptions:
- it is full of integers, in that it can be cast to an integer data type without changing value
- it is one-dimensional. Technically,
convolvewould raise an error if we didn’t, but it’s better to raise errors in a context where they can be clearly explained.convolvedoesn’t know anything about why this error is occuring, but we do and can communicate that to the user. - all of the elements are negative or positive.
None of these assumptions require any information that’s specific to this DecimalSequence.
Therefore, we can write this method as what’s called a staticmethod:
it is called without the “hidden” self argument.
This is achieved by writing @staticmethod above the definition of the method.
@staticmethod is called a decorator,
because it is added, like decoration,
on top of an existing function, method, or class,
in order to extend it.
While we’re at it, let’s add a doc-string to our class.
A doc-string is a string describing an object or function
that is intended to be displayed to users.
They can be viewed in IPython/Jupyter with the ? and ?? syntax.
class DecimalSequence():
"""A sequence of decimal digits representing an integer.
Digits are in the order they would be written: 123 -> [1, 2, 3].
A digit sequence ${x_i}$ of length $k$ in base b is mapped to an integer by
$\sum_i x_i b^{k-i}$
"""
def __init__(self, iterable):
self.check_iterable(iterable)
arr = np.atleast_1d(np.squeeze(np.asarray(iterable, dtype=np.int)))
self.arr = arr
self.base = 10
@staticmethod
def check_iterable(iterable):
error_msgs = ["(castable to) integers",
"one-dimensional",
"all negative or positive"]
arr = np.asarray(iterable, dtype=np.int)
error_checkers = [
lambda iterable: np.array_equal(arr, iterable),
lambda iterable: len(arr.shape) == 1,
lambda iterable: all([elem >= 0 for elem in iterable]) or
all([elem <= 0 for elem in iterable])]
for error_checker, error_msg in zip(error_checkers, error_msgs):
assert error_checker(iterable),
"DecimalSequences must be {}".format(error_msg)
...
def __mul__(self, other):
"""magic called by the expression `self * other`"""
if not isinstance(other, DecimalSequence):
raise TypeError("can't multiply DecimalSequence by object of type:"
.format(type(other)))
return DecimalSequence(np.convolve(self, other))
One small implementational note:
notice that the collection of errors and error messages is defined using lists,
rather than using a collection of try/catch blocks or if statements.
This style is easier to extend later (just add things to the lists)
and it cuts down on the amount of space taken by the code without harming readability.
Now, when a user, intentionally or not, tries some shenanigans with their inputs, we can catch the problem and give them a warning:
DecimalSequence([-1, 1]) * DecimalSequence([1, 1])
AssertionError: DecimalSequences must be all negative or positive
To int and Back Again
We have one problem remaining:
the result of multiplying two valid DecimalSequences is still
not guaranteed to be a valid DecimalSequence,
thanks to a problem noted in
the last blog post in this series:
DecimalSequence([1, 2, 3]) * DecimalSequence([4, 5])
array([ 4, 13, 22, 15])
We cannot write down 4132215 and mean the same thing as \(123 \times 45=5535\).
The problem is that when we turn a sequence of numbers into a single number, many sequences get mapped to the same number: \(\left[ 4, 13, 22, 15 \right]\) and \(\left[5, 5, 3, 5\right]\), for example.
That is, there are many equivalent representations
of a number as a sequence of smaller numbers,
and the valid DecimalSequence representation is just one.
Now, we could write a method that goes through a sequence and converts it, by hand, to its valid form. This is essentially done by “carrying”, as in “carry the one”. However, getting this exactly correct seems tricky to me – how are negative numbers to be handled, for example?
Instead, we’re going to make use of the fact that we can map back and forth between integers and sequences to get this “simplification” step for free!
We start by defining two methods:
one, from_int, to generate a DecimalSequence from an integer
and another, to_int, to generate an integer from a DecimalSequence.
from_int can be used to construct new DecimalSequences,
so it doesn’t make sense to have it as a typical method, attached to a specific sequence.
Luckily, there’s a decorator, @classmethod designed for this specific purpose.
It replaces the “hidden” self argument with a “hidden” cls (pronounced “class”) argument.
This argument refers to the class (here DecimalSequence), rather than a specific member.
That way, a user can write DecimalSequence.from_int(integer) and get a new DecimalSequence made from that integer.
to_int is a more standard method, so no need for decorators there.
We just need to write a Python version of the definition in our doc-string.
class DecimalSequence():
"""A sequence of decimal digits representing an integer.
Digits are in the order they would be written: 123 -> [1, 2, 3].
A digit sequence ${x_i}$ of length $k$ in base b is mapped to an integer by
$\sum_i x_i b^{k-i}$
"""
def __init__(self, iterable):
self.check_iterable(iterable)
arr = np.atleast_1d(np.squeeze(np.asarray(iterable, dtype=np.int)))
self.arr = arr
self.base = 10
@classmethod
def from_int(cls, intgr, base=10):
iterable = cls.int_to_iterable(intgr, base=base)
return cls(iterable)
def to_int(self):
return int(sum([elem * (self.base ** k) for k, elem
in enumerate(reversed(self))]))
@staticmethod
def int_to_iterable(intgr, base=10):
assert isinstance(intgr, int), "first argument must be integer"
iterable = []
while intgr > 0:
val = intgr % base
iterable.append(val)
intgr = intgr // base
return list(reversed(iterable))
...
def __mul__(self, other):
"""magic called by the expression `self * other`"""
if not isinstance(other, DecimalSequence):
raise TypeError("can't multiply DecimalSequence by object of type:"
.format(type(other)))
return DecimalSequence(np.convolve(self, other))
As you can see from_int is a bit more complicated than to_int.
For that reason, we split out the meatier part,
converting the integer into an iterable suitable for constructing a DecimalSequence,
into its own function, int_to_iterable,
and then leave the construction step to our __init__ method.
And how exactly does this method work?
We walk from the right side of the digit to the left
by using the remainder or modulo operation, %.
This “indexes” the last element of the integer, and we append it to our iterable.
Then, we use floor division (//) to remove the last element.
The result is in reverse order, so we flip it around once we’re done.
Now, we can convert between DecimalSequences and integers:
print(DecimalSequence.from_int(123))
1*10**2 + 2*10**1 + 3*10**0
DecimalSequence([1, 2, 3]).to_int()
123
This suggests a natural test: sending an integer to its sequence representation and back shouldn’t change it:
intgr = 123
assert DecimalSequence.from_int(intgr).to_int() == intgr
reduceing Complexity with Algebra
We are now ready to write a reduce function that
simplifies our DecimalSequences and guarantees they are always valid.
By defining int_to_iterable as we did above,
we guaranteed that any DecimalSequence built from an integer will be valid.
So to coerce any sequence to be valid,
we just need to convert it to an integer and then convert the resulting integer back into a DecimalSequence!
Imagine lining up all sequences of integers and all integers in two rows,
then drawing an arrow from a sequence s to an integer x
if x == to_int(s).
Many arrows from different ss will converge onto the same x.
Then imagine drawing an arrow from every x to the valid sequence s
it is mapped to by from_int.
The diagram below shows what this might look like.
You’re encouraged to draw your own version to check your understanding!
Notice that multiple red arrows
(corresponding to the action of to_int)
converge on a single integer,
but that at most one blue arrow
(corresponding to the action of from_int)
touches each sequence.
Furthermore, only valid sequences are touched by an arrow.
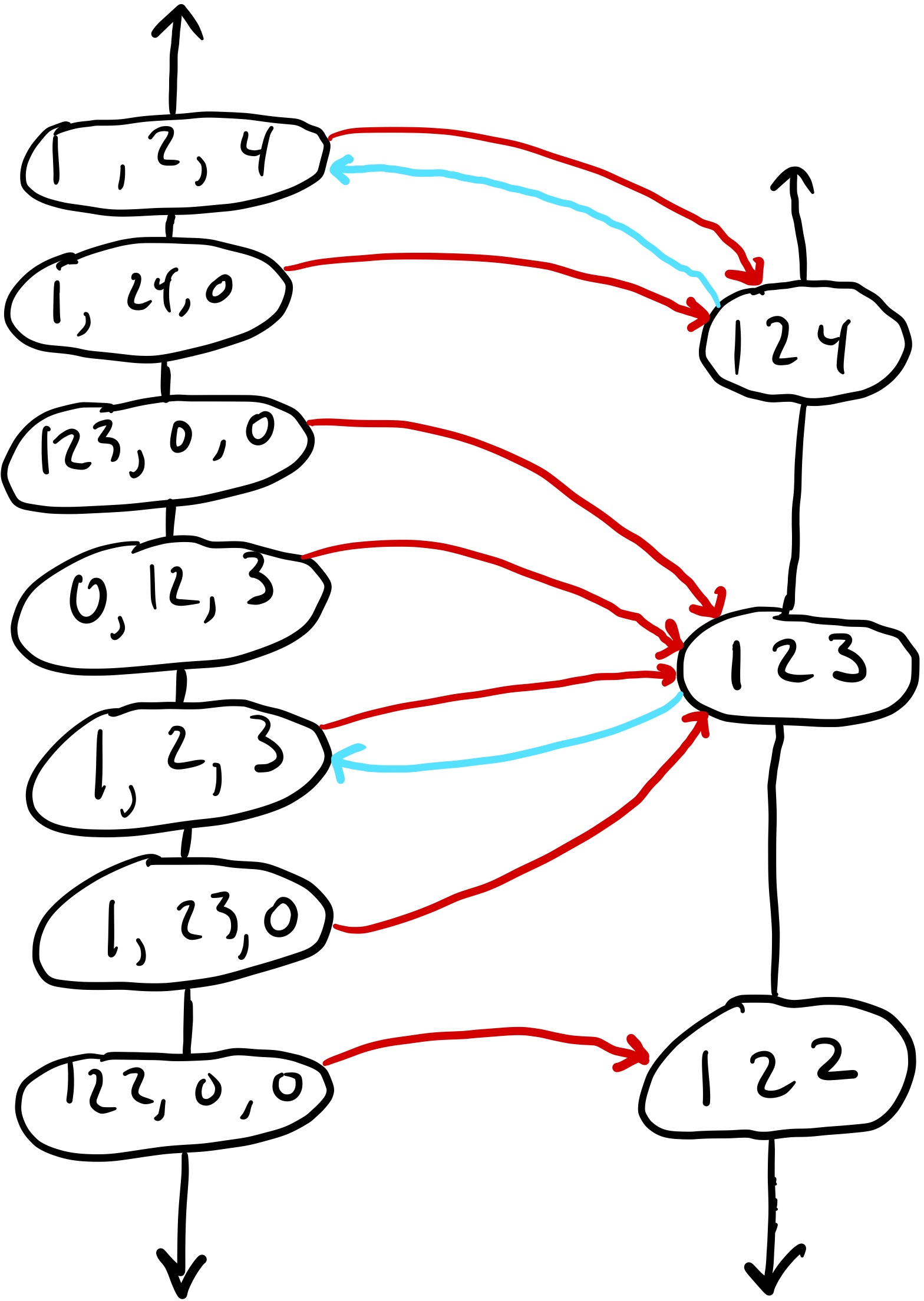
A function whose arrows, as drawn above, touch all of the objects on the other side is called a surjection. If multiple arrows land on the same object, the function is called many-to-one.
A function whose arrows, as drawn above, start from all of the objects on one side and never land on the same object on the other, the function is called an injection.
This motif, of a (often many-to-one) surjection followed by an injection, is extremely common in abstract algebra, where it appears in a variety of “decomposition theorems”: e.g. the Fundamental Theorem of Linear Algebra and the canonical decompositions of functions and of group homomorphisms. It’s also one way to understand the Singular Value Decomposition.
The key insight of these decomposition theorems is that even very complicated objects,
like the process that converts an invalid DecimalSequence to a valid one,
can often be decomposed into a few simpler objects,
which we can understand separately and then chain together.
For more on how abstract algebra can provide insight into programming problems, check out my blog post on functors and film strips or, if you really want to take the plunge, Category Theory for Programmers.
In the code block below,
we add a reduce method to our DecimalSequence class
that makes use of our “canonical decomposition” of the reduction operation.
We place it in the __init__ method so that all DecimalSequences are always in reduced form.
The only piece that’s not as described above is the first few lines of reduce,
which handle arrays that are already in reduced form
and arrays that start with a bunch of leading 0s.
class DecimalSequence():
"""A sequence of decimal digits representing an integer.
Digits are in the order they would be written: 123 -> [1, 2, 3].
A digit sequence ${x_i}$ of length $k$ in base b is mapped to an integer by
$\sum_i x_i b^{k-i}$
"""
def __init__(self, iterable):
self.check_iterable(iterable)
arr = np.atleast_1d(np.squeeze(np.asarray(iterable, dtype=np.int)))
self.arr = arr
self.base = 10
self.arr = self.reduce()
def reduce(self):
if all([len(str(elem)) == 1 for elem in self]):
while len(self) > 1 and self[0] == 0:
self.arr = self[1:]
return self.arr
else:
return DecimalSequence.from_int(self.to_int()).arr
...
def __mul__(self, other):
"""magic called by the expression `self * other`"""
if not isinstance(other, DecimalSequence):
raise TypeError("can't multiply DecimalSequence by object of type:"
.format(type(other)))
return DecimalSequence(np.convolve(self, other))
Now when we multiply two DecimalSequences together,
the result is in the valid form!
DecimalSequence([1, 2, 3]) * DecimalSequence([4, 5])
array([5, 5, 3, 5])
Fixing a Bug, Easily
We are almost done with a nice, usable, extensible DecimalSequence class.
But there’s a problem! One of our methods has a bug:
DecimalSequence.from_int(-11)
array([], dtype=int64)
Our implementation of int_to_iterable was wrong!
When coming up with the algorithm, we neglected to consider how it would work on negative integers.
Luckily, we can fix this issue easily.
We wrote an algorithm that works for non-negative integers.
A negative integer is just a positive integer multiplied by a minus sign
and a negative DecimalSequence is just a positive DecimalSequence
with all the entries multiplied by a minus sign.
Therefore we can just add a short piece at the beginning of our int_to_iterable
method that checks whether an input is negative,
and, if so, convert it to a positive integer (multiply by -1).
Then, once our algorithm is done,
we can easily convert our result to a negative DecimalSequence
by multiplying each of the elements by -1.
class DecimalSequence():
"""A sequence of decimal digits representing an integer.
Digits are in the order they would be written: 123 -> [1, 2, 3].
A digit sequence ${x_i}$ of length $k$ in base b is mapped to an integer by
$\sum_i x_i b^{k-i}$
"""
def __init__(self, iterable):
self.check_iterable(iterable)
arr = np.atleast_1d(np.squeeze(np.asarray(iterable, dtype=np.int)))
self.arr = arr
self.base = 10
self.arr = self.reduce()
def reduce(self):
if all([self.check_element(elem) for elem in self]):
while len(self) > 1 and self[0] == 0:
self.arr = self[1:]
return self.arr
else:
return DecimalSequence.from_int(self.to_int()).arr
def check_element(self, elem):
return -self.base < elem < self.base
...
@staticmethod
def int_to_iterable(intgr, base=10):
assert isinstance(intgr, int), "first argument must be integer"
sign = 1
if intgr < 0:
sign *= -1
intgr *= -1
iterable = []
while intgr > 0:
val = intgr % base
iterable.append(val)
intgr = intgr // base
iterable = [sign * elem for elem in iterable]
return list(reversed(iterable))
...
def __mul__(self, other):
"""magic called by the expression `self * other`"""
if not isinstance(other, DecimalSequence):
raise TypeError("can't multiply DecimalSequence by object of type:"
.format(type(other)))
return DecimalSequence(np.convolve(self, other))
DecimalSequence.from_int(-11)
array([-1, -1])
This is a very similar principle to the one we used to solve the reduce operation!
We had a working int_to_iterable method on a certain set of inputs,
and we wanted to extend it to cover more.
Instead of coming up with a more complicated method
to solve the int_to_iterable problem
on this expanded set of inputs,
we made a map from the inputs on which our method didn’t work
to the inputs on which it did,
and then a map from the outputs of the working method
to the desired outputs for the full method.
Again, we broke a complicated mapping down into simpler maps,
then combined them.
I include this bugfix only partly for pedagogical reasons, in order to work through another example where thinking algebraically and compositionally paid dividends, but also because this actually happened while I was working the problem out myself!
A minor implementational note:
this bugfix also required a change to the part of the reduce operation
that handles checking whether an array is already reduced,
since that was also not designed to handle negative integers.
Testing
Finally, we should write a test for our code.
Now that we have a map from integers to DecimalSequences,
we can check that mapping an integer to a sequence,
then multiplying,
and then mapping back to an integer
gives the same result as just multiplying the integers.
Algebraically, this is essentially a test that our map to DecimalSequence is a
homomorphism
with respect to multiplication.
import random
def assert_mul_correct(a, b):
seq_a, seq_b = DecimalSequence.from_int(a), DecimalSequence.from_int(b)
assert (seq_a * seq_b).to_int() == a * b
ints = list(range(-10000, 10000))
test_size = 100
[assert_mul_correct(random.choice(ints), random.choice(ints))
for _ in range(test_size)];
Conclusion
There’s much more to do to make a really excellent DecimalSequence type.
For one, you can hook into +, - and / with __add__, __sub__, and __div__.
For another, it’s sensible to multiply DecimalSequences with ints,
which requires extending the __mul__ method to do some type-checking and casting
(and don’t forget about __rmul__!).
Lastly, a DecimalSequence is just a specific instantiation of a generic
DigitSequence type, which would allow for different choices of (positive-valued) base.
These would all make fun projects to test your understanding of magic methods
and digit sequences in Python!