Answer
Central pattern generators or CPGs are collections of neurons that produce rhythmic behavioral outputs.
Due to the fundamental nature of rhythms, both in biology and in mathematics, we should expect to find many examples of central pattern generators (CPGs) in neuroscience.
One of the best-studied CPGs is the cat locomotion pattern generator, which was discovered over 100 years ago by pulling the brains out of cats!
Rhythms
The behavior of animals extends in time. In many cases, this behavior is repetitive: it could be extended forever, with some basic template occurring over and over again, beginning and ending in the same way: we walk by stepping left-right-left-right-left-…, fish swim by contracting one side of their body, then the other, birds fly by flapping their wings up and down and up again, and so on. Even outside of nature, inside our computers, some of the most fundamental steps of computation, the clock cycle of the CPU and the core loop of the operating system, are repeated actions.
Rhythms are fundamental because they express one of the basic ways a process can unfold over an arbitrary amount of time. In a very real way, it represents one of only three basic options for the behavior of a arbitrarily-long process: it can either continue to increase in intensity forever, it can settle down to some specific value and stay there forever, or it can oscillate, repeating itself over and over again.
The first option is impossible for biological processes: it is simply unphysical for anything to truly grow without bound, since we live in a finite universe†. At best, this can occur approximately over some regime, as in the population growth of bacteria in a dish or in the upstroke of the action potential.
Settling to a particular value is the definition of homeostasis, meaning our second option is in fact an important function of a myriad of biological processes.
Before returning to oscillations, I'd be remiss if I didn't note that there is a fourth, more complex, option for infinite-time behavior: chaos, where small changes slowly grow, as in the proverbial butterfly that causes a hurricane, while big changes get smeared out into nothing. Though chaos plays a role in biology, e.g. in the developing embryo, as discovered by Alan Turing, a role for chaotic dynamics in the brain is controversial in the field.
So, if we wish to generate an action, like walking, swimming, chewing, or flying, that repeats itself ad infinitum, or at least until we decide to stop, rather than varying chaotically, growing forever, or slowly petering out, we'd do well to make use of oscillations.
Put another way: our neurons must generate patterns of oscillatory behavior, so we should expect to find pattern generators that oscillate in the central nervous system. We call these central pattern generators.
A Model CPG
We model our neurons using a toolset from classical mechanics: dynamical systems. In brief, a dynamical system is any system that can be described with a differential equation, or an equation that describes how the system changes at each point in time.
Differential equations are fundamental mathematical objects: in a very real way, \(e\), \(\pi\), and the Gaussian, or Normal, distribution arise from differential equations. They are also critical for computational neuroscience and neurobiology. The Hodgkin-Huxley equations, which describe the evolution of the action potential, are differential equations. The leaky integrate-and-fire model of the neuron is a differential equation.
Because of their importance, their generality, and their fundamental nature, differential equations are a difficult subject, and notoriously so. But for the exact same reason, there exist simple, intuitive ways of explaining much of the critical understanding about the behavior of systems governed by these equations.
Consider the following idealized neural circuit:
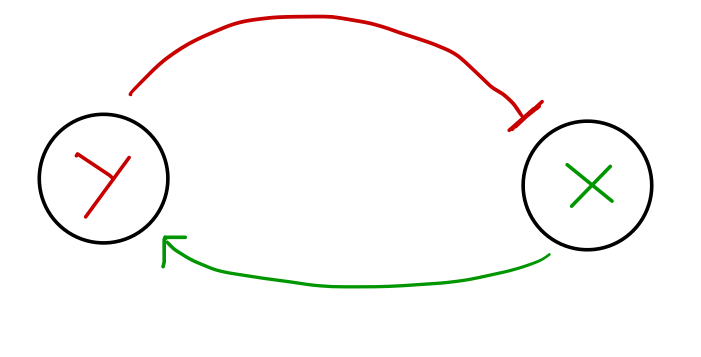
Neuron X activates Neuron Y, but Neuron Y inhibits Neuron X. Any time Neuron X becomes active, it will increase the activity of Neuron Y, which will eventually decrease the activity of Neuron X until it is below its baseline value. At that point, Neuron Y is no longer receiving as much activation from Neuron X, and so its activity goes down. This will eventually cause the activity of Neuron X to increase again, starting the whole cycle over again.
Just from that explanation, it is clear that this system is oscillatory. We can understand it even more clearly if we use the methods of dynamical systems analysis pioneered by Poincaré to describe the motion of the planets.
We represent the activity of a neuron by a single number: large and positive means more active than baseline, while large and negative means less active than baseline. This means our baseline activity is represented by 0.
We translate the notions of "activation" and "inhibition" into mathematics like this:
\[\begin{align} \frac{dX}{dt} &= -Y \\ \frac{dY}{dt} &= X \end{align}\]In English, you might read the second equation as: "the change in the activity of Y over time is equal to the current activity of X", or "activity in X causes the activity in Y to increase or decrease proportionally".
For any pair of values X and Y, representing a possible state for the two neurons, we can then describe how the state will change over time. To each pair, we can attach an arrow, pointing towards what the values will look like in the next instant.
If we treat X and Y as an ordered pair and draw our arrows on the Cartesian plane, we get a picture of the system called a flow field or a phase portrait.
The phase portrait for our neural circuit appears below:
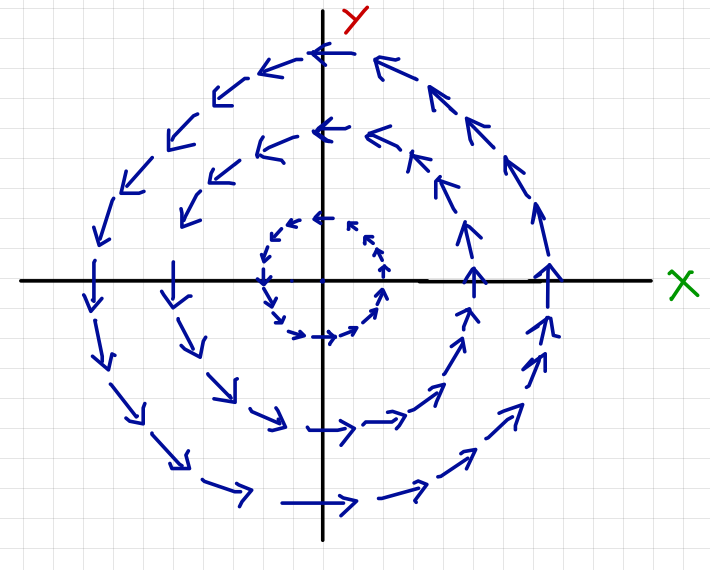
The blue arrows represent the pair of values \(\frac{dX}{dt}\) and \(\frac{dY}{dt}\) – they are vectors. You should confirm for yourself that the values match up!
Phase portraits are useful because we can see what the behavior of a system looks like without having to do any number-crunching. Just by looking at the portrait, we can see that, if we start off with either X or Y away from its baseline value, the neurons will "go in circles": first one will increase while the other decreases, then vice versa.
Put your finger on the x-axis, and then follow the arrows side to side, without leaving the x-axis. That is, move left when the arrows point left, ignoring whether they also point up or down, and move right when the arrows point right. Your finger should move back and forth from the starting point to minus the starting point, and then back again. It is oscillating. In fact, it's drawing a sine or cosine wave!
If you're the programming type, you might understand this better by means of the following Python code:
dt = 0.0001
x = 5; x = 0
for ii in range(aBigNumber):
x = x + -y*dt
y = y + x*dtTry coding that up in your favorite programming language
and plotting the resulting x and y values.
You should get circles, so long as dt is small
and aBigNumber is big!
We can see how such a neural circuit might be used for movement generation by connecting the neural activity values to motor commands.
Let's say that X is a speed-representing neuron, meaning that increased spiking activity in X tends to cause an increase in the speed that some muscle or group of muscles is moving. For concreteness' sake, let's say it's the muscles birds use to flap their wings.
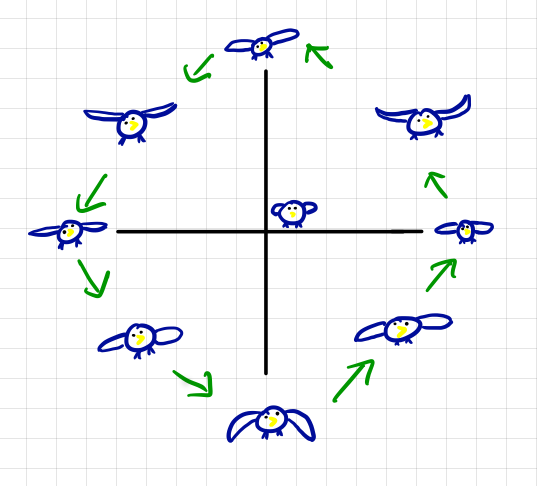
In the above diagram, I've drawn how the state of a bird using a neuron like X to flap its wings will change over time. If the neurons are both at their baseline activity, then nothing happens, represented by the single bird at the origin. But if some signal comes from another neuron and increases the activity of neuron X, then the bird's wings begin to flap, first up, then down, and then back again. If nothing changes, the bird will continue to fly forever, but if another signal comes in and returns X and Y to 0, then the bird's wings will stop flapping.
An Actual CPG: Cats!
Interestingly, the pattern generators for locomotion are not necessarily located within the brain. This was discovered when a group of neuroscientists removed the entire brain of cat, then placed it on a treadmill. It still walked! Click the image below to see a video.
In fact, as long as 100 years ago, it was known that one could "decerebrate" (that is, cut the brain out of) a cat, cut its spinal cord, and even sever most of the sensory nerves, and it will still respond appropriately to stimuli, like a treadmill, that encourage motion.
This indicated that the central pattern generators were to be found in the ventral horn of the spinal cord.
Additional experiments showed that, even when the muscles were paralyzed, rhythmic activity occurred in response to motion-generating stimuli, detected using extracellular electrophysiology.
References
For understanding dynamical systems, the classic text is Nonlinear Dynamics and Chaos, by Steven Strogatz. I learned about these systems in the context of biology, and my professor for that course, Dmitry Kondrashov, has written a book introducing the ideas to biologists, developing all the mathematical machinery necessary in as clear a fashion as possible.
For more concrete information on CPGs, check out this review from 1998 by Duysens and Van de Crommert.
Footnotes
† An astute reader might note that, thanks to the second law of thermodynamics, oscillating forever and staying at one value forever are impossible, since they require energy and can be used to perform work. While this view is technically correct, it misses a subtle difference in the timescale of failure for a system trying to oscillate forever versus one trying to grow forever.
Eternal growth compounds, meaning that even modest continual growth will quickly spiral out of control, reach values that are orders of magnitude greater than the initial state in a reasonable amount of time – compounding growth reaches exponential values in only linear time.
Oscillation, on the other hand, can proceed with miniscule amounts of energy, especially compared with the amount of energy available in the entire Universe. Eventually, sure, there won't even be enough energy to vibrate a guitar string, but a guitar string could vibrate many, many trillions of times before that happens. On the other hand, just 64 periods of doubling is enough to go from the scale of a grain of rice to the interstellar scale.
